Two Pointers

The two pointers method iterates two pointers across an array, to track the start and end of an interval, or two values in a sorted array that we are currently checking.Both pointers are monotonic; meaning each pointer starts at one end of the array and only move in one direction.

2 SUM Problem

Given an array of N elements (1 ≤ N ≤ 105), find two elements that sum to X. We can solve this problem using two pointers; sort the array, then set one pointer at the beginning and one pointer at the end of the array. Then, we consider the sum of the numbers at the indices of the pointers. If the sum is too small, advance the left pointer towards the right,and if the sum is too large, advance the right pointer towards the left. Repeat until either the correct sum is found, or the pointers meet (in which case there is no solution).

Let’s take the following example array, where N = 6 and X = 15

First, we sort the array:

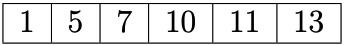
We then place the left pointer at the start of the array, and the right pointer at the end of the array.

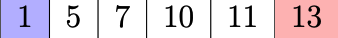
Then, run and repeat this process: If the sum of the pointer elements is less than X,move the left pointer one step to the right. If the sum is greater than X, move the right pointer one step to the left. The example is as follows. First, the sum 1 + 13 = 14 is too small, so we move the left pointer one step to the right.

Now, 5 + 13 = 18 overshoots the sum we want, so we move the right pointer one step to the left.

At this point we have 5 + 11 = 16, still too big. We continue moving the right pointer to the left.

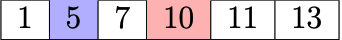
Now, we have the correct sum, and we are done.

Code is as follows:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int left =0;
int right=n-1;
while(left<right){
    if(arr[left]+arr[right]==x){
        break;
    }
    else if(arr[left]+arr[right]<x){
        left++;
    }
    else{
        right++;
    }
}
//if left>=right after the loop ends,no answer exists

Subarray Sum

Given an array of N (1 ≤ N ≤ 105) positive elements, find a contiguous subarray that sums to X.

We can do this in a similar manner to how we did the 2SUM problem: except this time we start both pointers at the left, and the pointers mark the beginning and end of the subarray we are currently checking. We advance the right pointer one step to the right if the total of the current subarray is too small, advance the left pointer one step to the right if the current total is too large, and we are done when we find the correct total.

Maximum subarray sum

Another problem that isn’t quite solved by two pointers, but is somewhat related, is the maximum subarray sum problem.

Given an array of N integers (1 ≤ N ≤ 105), which can be positive or negative, find the maximum sum of a contiguous subarray.We can solve this problem using Kadane’s algorithm, which works as follows: we iterate through the elements of the array, and for each index i, we maintain the maximum subarray sum of a subarray ending at i in the variable current, and the maximum subarray sum of a subarray ending at or before i, in the variable best.

Example code is below.

1
2
3
4
5
int best=0,current=0;
for(int i=0;i<n;i++){
    current=max(0,current+arr[i]);
    best=max(best,current);
}

Line sweep

Line sweep is the technique of sorting a set of points or line segments and then processing them in order (this usually means from left to right). The name line sweep comes from the fact that we are sweeping an imaginary vertical line across the plane containing the points or segments.

To describe this technique, we’ll be using the 2019 US Open problem, “Cow Steeplechase II”.

In this problem, we are given some line segments and asked to find one line segment and remove it such that the resulting segments form no intersections. It is guaranteed that this is always possible.

First of all, let’s observe it is sufficient to find any two line segments that intersect. Once we have done this, the solution is guaranteed to be one of these two segments. Then, out of the two, the segment with multiple intersections is the answer (because removing any other segment decreases the number of intersections by at most 1, and only removing the segment with multiple intersections ensures there are no intersections).

If both segments have one intersection, that means the intersect with each other, so we should return the one with the smallest index (as per the problem statement). Now, the problem reduces to two parts: checking if two line segments intersect, and processing the line segments using a line sweep.

Checking If Two Segments Intersect

To check if two line segments intersect, we will use a fact from algebra: if we have the points A=(X_a,Y_a),B=(X_b,Y_b)and C=(X_c,Y_c) then the (signed) area of ▵ABC,denoted [ABC],is (X_b-X_a)(Y_c-Y_a)-(X_c-X_a)(Y_b-Y_a)This can be derived from the cross product of the vectors $\overrightarrow{AB}$ and $\overrightarrow{AC}$.

The part that will help us is the fact that this area is signed, which means that [ABC] is

positive if A, B, and C occur in counterclockwise order,

negative if A, B, and C occur in clockwise order, and

zero if A, B, and C are collinear.

Then, the key observation is that two segments $\overrightarrow{PQ}$ and $\overrightarrow{XY}$ intersect if the two conditions hold:

• [XPQ] and [YPQ] have different signs
• [PXY] and [QXY] have different signs

For example, in the figure below, [X₁P₁Q₁] and [Q₁X₁Y₁]are positive because their vertices occur in counterclockwise order, and [Y₁P₁Q₁] and [P₁X₁Y₁] are negative because their vertices occur in clockwise order. Therefore, we know that X1Y1 and P1Q1 intersect. Similarly, on the right, we know that [P₂X₂Y₂] and [Q₂X₂Y₂] have vertices both going in clockwise order, so their signed areas are the same, and therefore P₂Q₂ and X₂Y₂ don’t intersect.

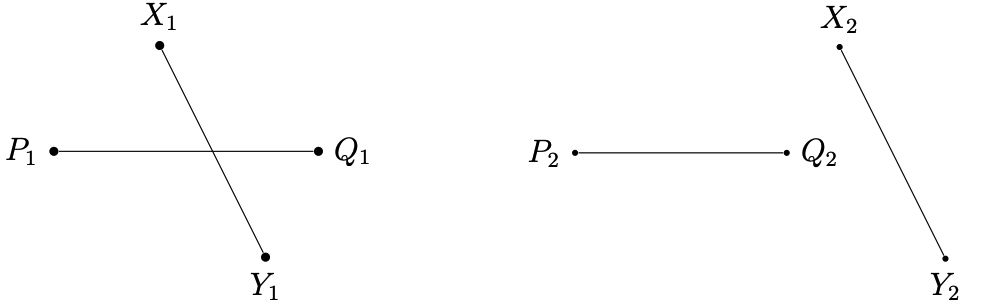
If the two conditions hold and some of the signs are zero, then this means that the segments intersect at their endpoints. If the problem does not count these as intersecting, then consider zero to have the same sign as both positive and negative.

However, there is a special case. If the signs of all four areas are zero, then all four points lie on a line. To check if they intersect in this case, we just check whether one point is between the others. In particular, we check if P or Q is on XY or if X is on P Q. We don’t need to check if Y is on P Q because if the segments do intersect, we will have two instances of points on the other segments.

Here’s a full implementation:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
struct Point{
    int x,y
    Point(int xst,int yst):x(xst),y(yst)
    {

    }
};
int sign(Point A,Point B,Point C){
    int area =(B.x-A.x)*(C.y-A.y)-(C.x-A.x)*(B.y-A.y);
    if(area>0){
        return 1;
    }
    if(area<0){
       return -1; 
    }
}
bool between(Point P,Point X,Point Y){
    return ((X.x <= P.x && P.x <= Y.x) || (Y.x <= P.x && P.x <= X.x))&& ((X.y <= P.y && P.y <= Y.y) || (Y.y <= P.y && P.y <= X.y));
}
bool intersectQ(Point P, Point Q, Point X, Point Y) {
int signs[4]={sign(P,X,Y), sign(Q,X,Y), sign(X,P,Q), sign(Y,P,Q)};
 if (signs[0] == 0 && signs[1] == 0 && signs[2] == 0 && signs[3] == 0){
      return between(P,X,Y)||between(Q,X,Y)||between(X,P,Q);
    }
    return signs[0]!=signs[1]&&signs[2]!=sign[3];
}

Processing Line Segments

Let’s break apart the N line segments into 2N events, one for each start and end point. We’ll store whether some event is a start point or an end point, and which start points correspond to each end point.

Then, we process the endpoints in order of x coordinate from left to right, maintaining a set of currently processed segments, which is sorted by y. When we hit an endpoint, we either add or remove a segment from the set, depending on whether we start or end a segment.Every time we add a segment, we check it for intersection with the segment above it and the segment below it. In addition, every time we remove a segment, we check the segment above it and the segment below it for intersection. Once we find an intersection, we are done.

Bitwise Operations and Subsets

Binary Representations of Integers

In programming, numbers are stored as binary representations. This means that a number x is represented as

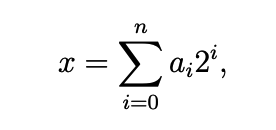
where the a_is are either 0 or 1 and n = [b log₂ x]

For example: 17 = 2⁴+2⁰ = 10001₂

Each digit in the binary representation, which is either 0 or 1, is called a bit.

Bitwise Operations

There are several binary operations on binary numbers called bitwise operations. These operations are applied separately for each bit position. The common binary operations are shown in table

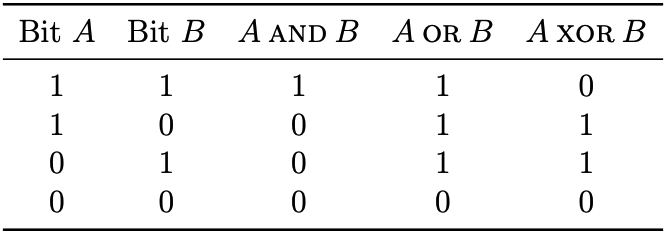
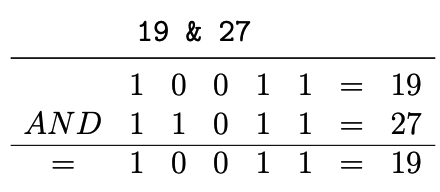
The AND operation (&) returns 1 if and only if both bits are 1.

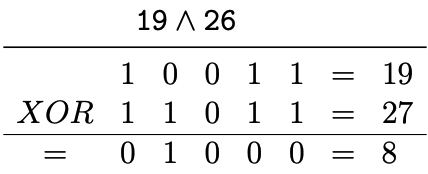
The XOR operation ( ∧ ) returns 1 if and only if exactly one of the bits is 1.

Finally, the left shift operator x « k multiplies x by 2^k. Watch for overflow and use the long long data type if necessary. For example:

Exercises

(a) 19 & 34 (Answer: 2)
(b) 14 | 29 (Answer: 31)
(c) 10 ∧ 19 (Answer: 25)
(d) 3 « 5 (Answer: 96)

Generating Subsets

Occasionally in a problem we’ll want to iterate through every possible subset of a given set, either to find a subset that satisfies some condition, or to find the number of subsets that satisfy some condition. Also, some problems might ask you to find the number of partitions of a set into 2 groups that satisfy a certain condition. In this case, we will iterate through all possible subsets, and check each subset for validity (first adding the non-selected elements to the second subset if necessary).

In a set of N elements, there are 2^N possible subsets, because for each of the N elements,there are two choices: either in the subset, or not in the subset. Subset problems usually require a time complexity of O(N·2^N), because each subset has an average of O(N) elements.

Now, let’s look at how we can generate the subsets. We can represent subsets as binary numbers from 0 to 2^N − 1. Then, each bit represents whether or not a certain element is in the subset. Let’s look at an example set of a, b, c.

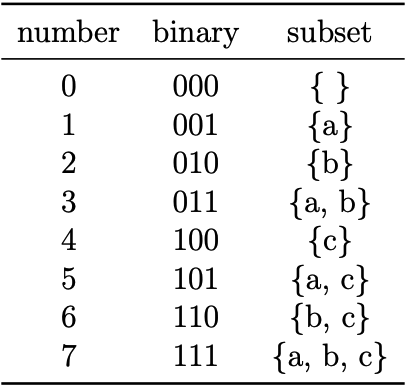
Algorithm: The algorithm for generating all subsets of a given input array

1
2
3
4
5
6
7
8
9
10
11
Function generateSubsets
Input:An array arr, and its length n
for i ← 0 to 2^n -1 do
    Declare list
        for j = 0 to n-1 do
            if the bit in the binary representation of i corresponding to 2 j is 1 then
                Add arr[j] to the list
            end
        end
    Process the list
end

In the following code, our original set is represented by the array arr[] with length n.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
int ans = 0;
for(int i = 0; i < (1<<n); i++){
// this loop iterates through the 2^n subsets, one by one.
// 1 << n is a shortcut for 2^n
    vector<int> v;
    // we create a new list for each subset and add
    // the elements to it
    for(int j = 0; j < n; j++){
        if((i & (1 << j)) > 0){
        // (1 << j) is the number where only the bit representing 2^j is 1.
        v.push_back(j); // if the respective bit of i is 1,
        // add that element to the list
        }
    }

    if(valid(list)){
    // code is not included here, but this method will vary depending on the
    // problem to check if a certain subset is valid
    // and increments the answer counter if so.
    ans++;
    }
}

Ad-hoc

The silver division also often has ad hoc problems. They primarily rely on non-standard algorithmic thinking and problem solving ability. You develop these skills by solving problems;
thus, we don’t have much content to teach you about ad hoc problems, but we provide a selection of problems at the end of the chapter for your practice.

Problems

1. Two Pointers
   • Sum of Two Values
   • Maximum Subarray Sum
2. Line Sweep
   • Cow Steeplechase II
3. Subsets
   • Apple Division
   • Circular Barn
   • Left Out
   • Sleepy Cow Herding
   • Secret Cow Code
   • Berry Picking
   • Meetings

Happy Codeing 👨🏻‍💻