2P or not to 2P, No wait isn’t this just bs

1. Prefix sums

Given an array $a$ of $n$ elements, prefix sums allow you to calculate the sum of any range of elements $[l, r]$ $1 \leq l \leq r \leq n$ in $\mathcal{O}(1)$ constant time (with $\mathcal{O}(n)$ pre-processing).

The trick is to pre-calculate (to calculate once beforehand for multiple usages later) an array prefix, of cumulative sums. For each $i$ from $1$ to $n$, prefix[i] stores the sum a₁ + a₂ + ….. + a_i. Then, the sum of elements in the range [l, r] can be easily found out as prefix[r] - prefix[l-1].

Reading material:

• Peltorator [V] (Use english subtitles)
• USACO [B]
• 2D prefix sums - USACO [B]
• Range updates using prefix sums - Codeforces [B]

This page uses math latex formatting. Download the extension to render it.

2. Two pointers and sliding window

The two pointer or 2p technique, is an op technique that has the power to reduce an $\mathcal{O}(n^2)$ algorithm to an $\mathcal{O}(n)$ one.

Reading material:

• Two pointers - Quora [B] & CF EDU
• Sliding window - GFG [B]
• Sliding window applications - Medium [B]

3. Binary Search

Binary search is an even more op technique that has the power to reduce an $\mathcal{O}(n)$ algorithm to an $\mathcal{O}(logn)$ one. The catch is that this can only be used when the data is sorted by some property.

The most trivial use of binary search is to locate an element in a sorted array or report that it does not exist, in $\mathcal{O}(logn)$ where $n$ denotes the size of the array. See binary search for dummies if you are not familiar with the basic algorithm.

Binary search however, is much, much, more than that. When you find yourself in a tough spot with no way out, no light at the end of the tunnel and in complete darkness, ask yourself this

Can I binary search the answer?

More often than not, the answer will be yes. A glimmer of hope, a shimmering light that marks the end of the tunnel. You start to slowly piece together the solution bit by bit, as you near the exit step by step. You’ve reached the end, the brightness now overwhelming, salvation at last. Mankind has never received a greater gift than binary search. Binary search is the way. Binary search is always the answer. Binary search is in itself, a religion. Join the cult, you won’t regret it. Here are some inspiring quotes from our famous leaders

No more hunger, no more poverty. It’s all thanks to binary search.

– Mahatma Gandhi

It’s genius. I wish I just did a binary search from the start. Damn!

– Albert Einstein

Just binary search bro.

– Julius Caesar

What are you waiting for? Join the cult NOW! JK.

Binary search is not limited to just searching for an element. You can even binary search the optimal answer to a problem.

Consider this problem. Lets define a function $\mathrm{check}(x)$ that returns true if it is possible to make the answer at least $x$ in at most $k$ operations, otherwise false.

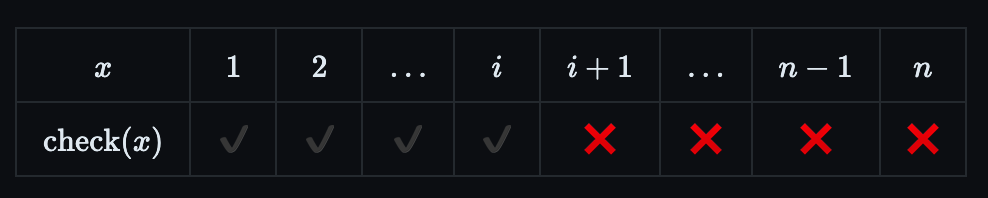
Observe that if $\mathrm{check}(x)$ is true then even $\mathrm{check}(x-1)$ must be true. Similarly, if $\mathrm{check}(x)$ is false then even $\mathrm{check}(x+1)$ must be false. This yields a property which appears to be sorted (first all trues, followed by all falses). What we are looking for is the largest value of $x$ for which $\mathrm{check}(x)$ returns true, which can be done with a simple binary search.

Here is my solution to the problem.

Reading material:

• The trivial algorithm - Medium [B]
• Binary search over the answer - Medium [B]
• A comprehensive tutorial
  • Errichto [V]
  • Topcoder [B]
  • CPH Ch 3, pg 31 - 34
• CF EDU on Binary search

This page uses math latex formatting. Download the extension to render it.

4. Ternary Search

Ternary Search is an extension of binary Search that allows you to locate the minima or maxima of a unimodal function.

Reading material:

• CP Algorithms [B] - try reading this. Very detailed explanation.
• HackerEarth [B]

Practice

Mashups of topic relevant problems spanning a range of difficulties.

Competitive Programming Beginner Topics Part 4