Elementary Number Theory

Prime Factorization

A number a is called a divisor or a factor of a number b if b is divisible by a, which means that there exists some integer k such that b = ka. Conventionally, 1 and n are considered divisors of n. A number n > 1 is prime if its only divisors are 1 and n. Numbers greater than 1 that are not prime are composite.

Every number has a unique prime factorization: a way of decomposing it into a product of primes, as follows:

n = p1a1 p2a2 · · · pkak

where the pi are distinct primes and the ai are positive integers.

Now, we will discuss how to find the prime factorization of an integer

Algorithm: Finds the prime factorization of a number

Function factor

Input: n, the number to be factorized
Output: v, a list of all the prime factors
1
2
3
4
5
6
7
8

v ← empty list
for i ← 2 to √n do
    while n is divisible by i do
        n ← n/i
        Add i to the list v
    end
end
return v;

This algorithm runs in O(√n) time, because the for loop checks divisibility for at most √n values. Even though there is a while loop inside the for loop, dividing n by i quickly reduces the value of n, which means that the outer for loop runs less iterations, which actually speeds up the code

Let’s look at an example of how this algorithm works, for n = 252. Tux, the Linux mascot

At this point, the for loop terminates, because i is already 3 which is greater than [√7]. In the last step, we add 7 to the list of factors v, because it otherwise won’t be added, for a final prime factorization of {2, 2, 3, 3, 7}.

GCD and LCM

The greatest common divisor (GCD) of two integers a and b is the largest integer that is a factor of both a and b. In order to find the GCD of two numbers, we use the Euclidean Algorithm, which is as follows:

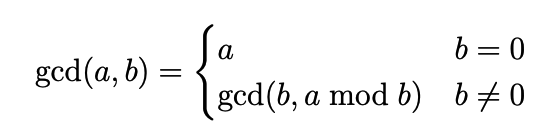
Tux, the Linux mascot

This algorithm is very easy to implement using a recursive function, as follows:

1
2
3
4
5
6

int gcd(int a, int b) {
    if (b == 0) {
        return a;
    }
    return gcd(b, a % b);
}

Finding the GCD of two numbers can be done in O(log n) time, where n = min(a, b).

The least common multiple (LCM) of two integers a and b is the smallest integer divisible by both a and b.

The LCM can easily be calculated from the following property with the GCD:

lcm(a,b)=a*b/gcd(a,b)

If we want to take the GCD or LCM of more than two elements, we can do so two at a time,in any order. For example,

gcd(a1,a2,a3,a4)=gcd(a1,gcd(a2,gcd(a3,a4)))

Modular Arithmetic

In modular arithmetic, instead of working with integers themselves, we work with their remainders when divided by m. We call this taking modulo m. For example, if we take m = 23, then instead of working with x = 247, we use x mod 23 = 17. Usually, m will be a large prime, given in the problem; the two most common values are 109 + 7, and 998 244 353.Modular arithmetic is used to avoid dealing with numbers that overflow built-in data types,because we can take remainders, according to the following formulas:

(a + b) mod m = (a mod m + b mod m) mod m

(a − b) mod m = (a mod m − b mod m) mod m

(a · b) (mod m) = ((a mod m) · (b mod m)) mod m

ab mod m =(a mod m)b mod m

Problems

If you Need more information Read this blog:

Happy Codeing 👨🏻‍💻